how to find angle between two vectors
Angle between two vectors
Page Navigation:
- Angle between two vectors - definition
- Angle between two vectors - formula
- Examples of tasks
- plane tasks
- spatial tasks
Definition. The angle between two vectors, deferred by a single point, called the shortest angle at which you have to turn around one of the vectors to the position of co-directional with another vector.
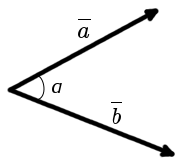
Basic relation. The cosine of the angle between two vectors is equal to the dot product of this vectors divided by the product of vector magnitude.
Angle between two vectors - formula
Examples of tasks
Examples of plane tasks
Example 1. Find the angle between two vectors a = {3; 4} and b = {4; 3}.
Solution: calculate dot product of vectors:
a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Calculate vectors magnitude:
|a| = √32 + 42 = √9 + 16 = √25 = 5
|b| = √42 + 32 = √16 + 9 = √25 = 5
Calculate the angle between vectors:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |
Example 2. Find the angle between two vectors a = {7; 1} and b = {5; 5}.
Solution: calculate dot product of vectors:
a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Calculate vectors magnitude:
|a| = √72 + 12 = √49 + 1 = √50 = 5√2
|b| = √52 + 52 = √25 + 25 = √50 = 5√2
Calculate the angle between vectors:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| |a| · |b| | 5√2 · 5√2 | 50 | 5 |
Examples of spatial tasks
Example 3. Find the angle between two vectors a = {3; 4; 0} and b = {4; 4; 2}.
Solution: calculate dot product of vectors:
a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Calculate vectors magnitude:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5
|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Calculate the angle between vectors:
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |
Example 4. Find the angle between two vectors a = {1; 0; 3} and b = {5; 5; 0}.
Solution: calculate dot product of vectors:
a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Calculate vectors magnitude:
|a| = √12 + 02 + 32 = √1 + 9 = √10
|b| = √52 + 52 + 02 = √25 + 25 = √50 = 5√2
Calculate the angle between vectors:
| cos α = | a · b | = | 5 | = | 1 | = | √5 | = 0.1√5 |
| |a| · |b| | √10 · 5√2 | 2√5 | 10 |

how to find angle between two vectors
Source: https://onlinemschool.com/math/library/vector/angl/
Posted by: robertscatill93.blogspot.com

0 Response to "how to find angle between two vectors"
Post a Comment